Оглавление
Исходные данные.
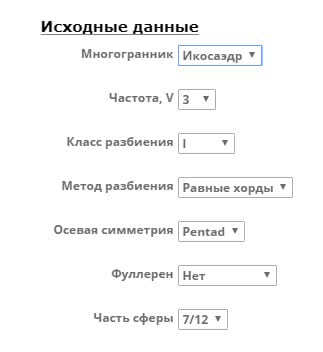
Область «Исходные данные» предназначена для задания геометрии каркаса. Можно изменять параметры в следующих полях:
«Многогранник» — многогранник на основание которого строится вся конструкция. Возможны два варианта: икосаэдр и октаэдр.
«Частота, V» — количество разбиений вершин. При увеличении частоты, увеличивается количество вершин и ребер соответственно. Чем больше это значение, тем больше форма каркаса приближается к сфере и тем меньше длина рёбер.
Икосаэдр — многогранник, у которого значение частоты разбиения V равно 1.
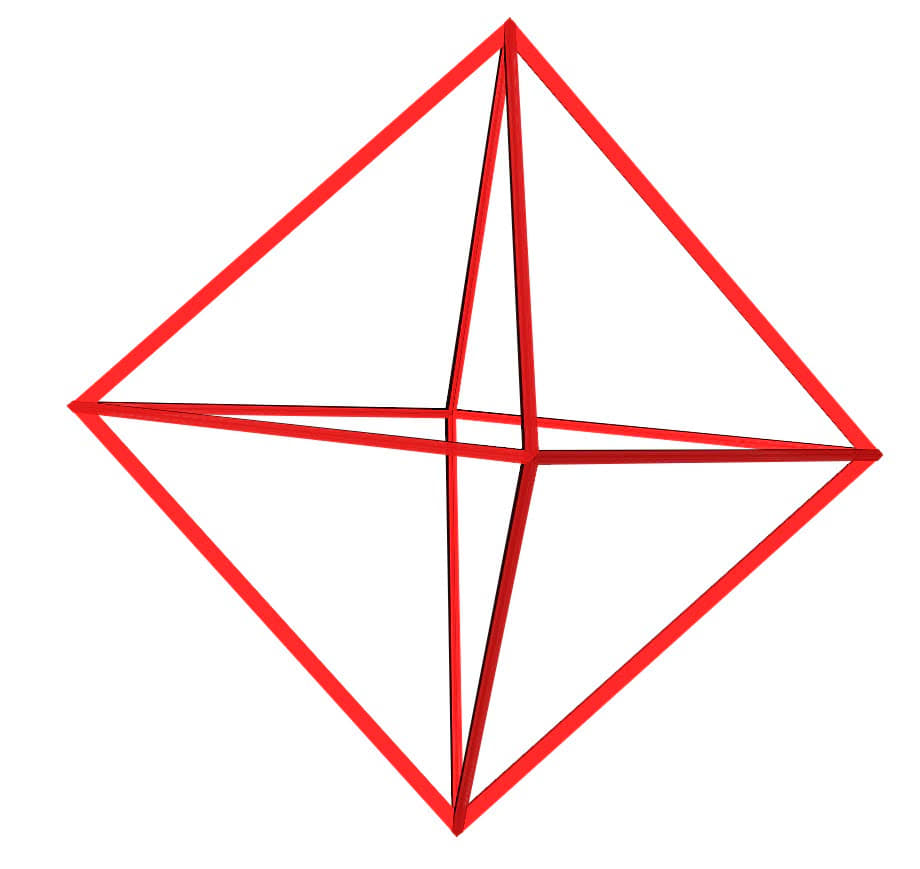Октаэдр — многогранник, у которого значение частоты разбиения V равно 1.
Значение частоты разбиения равное единице соответствует конструкции в виде икосаэдра или октаэдра в зависимости от того какой многогранник задан в графе «многогранник». При увеличении частоты происходит разбиение рёбер многогранника на части. Количество рёбер, составляющих разбитое ребро, равно частоте разбиения.
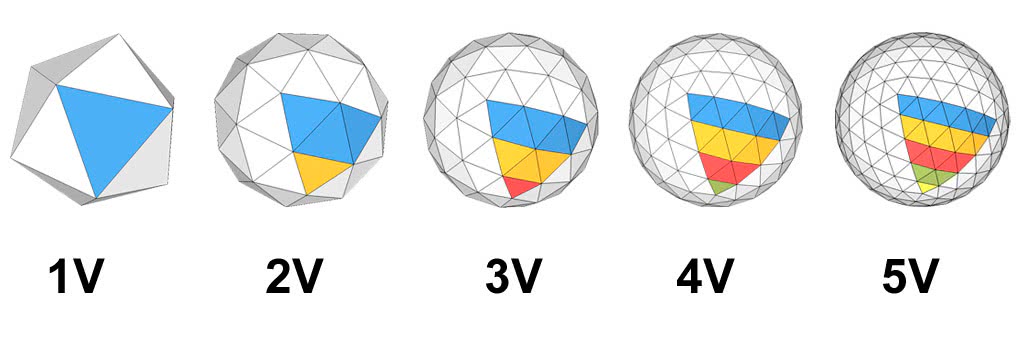Частота разбиения икосаэдра.
«Класс разбиения» — этот пункт отвечает за выбор способа разбиения, а следовательно и формы конечной конструкции.
При частоте разбиения равной двум и более возможны различные варианты каждого разбиения. Эти варианты делятся на классы. Если спроецировать разбиение на грань икосаэдра, то все возможные классы разбиения икосаэдра можно представить в виде схемы.
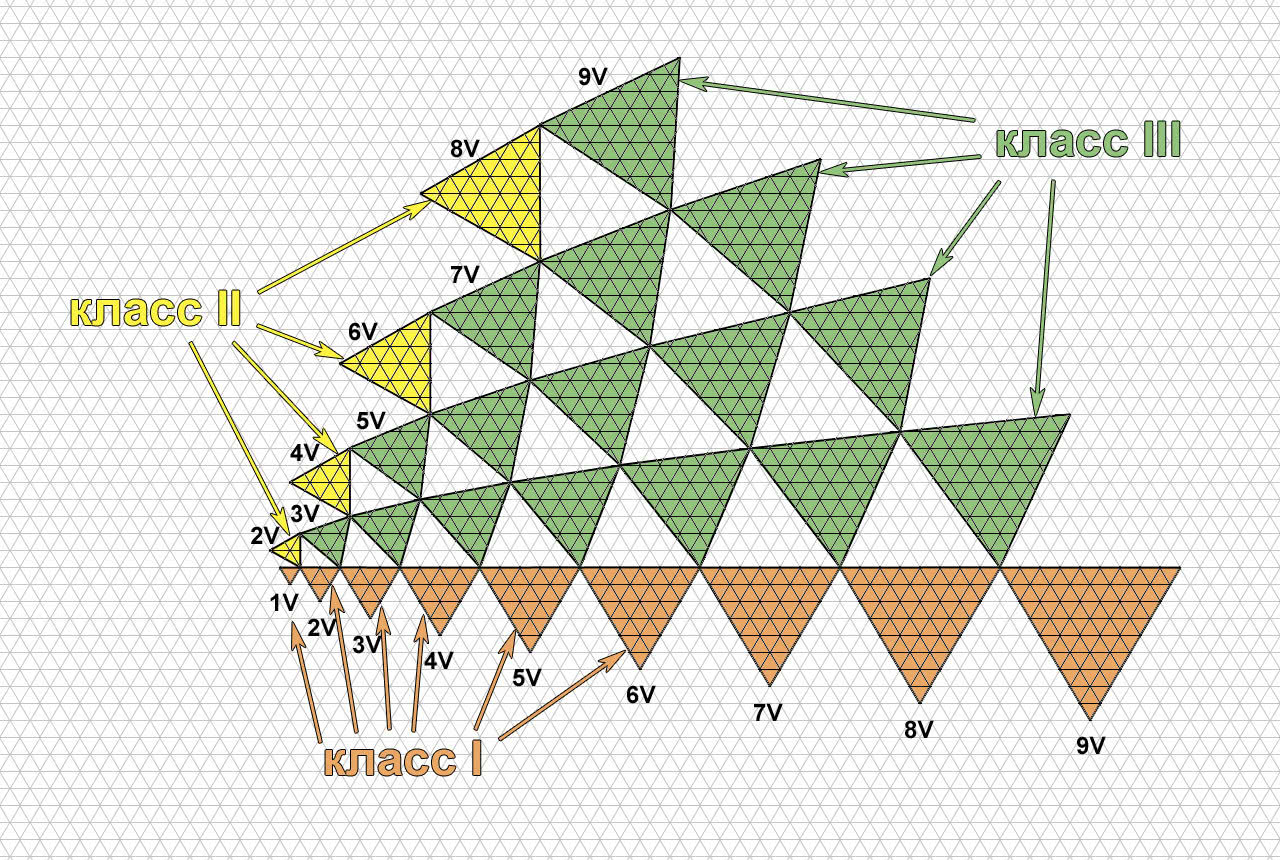Классы разбиения купольных конструкций.
В калькуляторе римскими цифрами обозначены основные классы, всего их три. Арабскими цифрами обозначены вариации основных классов.
Аналогично способы разбиения задаются для октаэдра.
«Метод разбиения» — позволяет сделать выбор между «Равные хорды», «Равные дуги» и «Мексиканец».
«Осевая симметрия» — выбор оси симметрии, которая учитывается при отсечении части купола от сферы и выстраивании купола по вертикали. Возможные варианты:
- Pentad — ось симметрии проходит через вершину, в которой сходится 5 рёбер.
- Cross — ось симметрии проходит через вершину, в которой сходится 6 рёбер.
- Triad — ось симметрии проходит через грань.
«Фулерен» — выбор формы купола в виде фулерена, который вписывается («вписанный») в сферу, или описывает её («описанный»). Поле «Фулерен» не доступно при выборе варианта соединения «Joint».
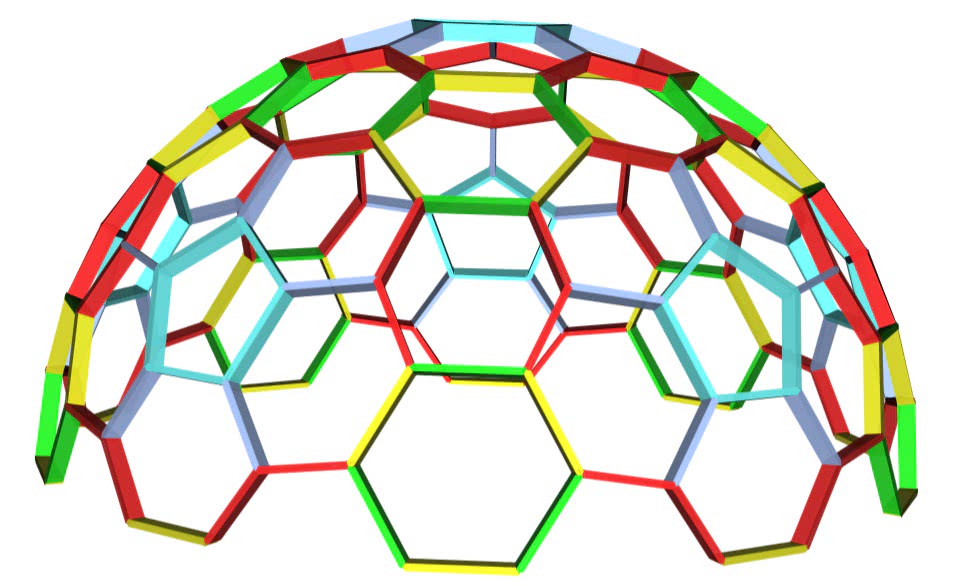купол в форме фулерена
«Выравнивание основания» — позволяет выравнивать основание относительно плоскости основания за счет изменения длин рёбер у основания купола. Поле «Выравнивание основания» не доступно при выборе способа соединения «Cone» или выборе формы фулерена.
Функция «выравнивание основания» изменят длину рёбер у основания купола таким образом, что вершины купола на внешней его поверхности располагаются в плоскости основания. Вершины купола на внутренней поверхности купола в общем случае не располагаются в плоскости основания, а строятся по общему принципу — к центру купола от его внешней поверхности.
При включении «выравнивания основания» рёбра своей широкой стороной лежат в плоскости горизонта в случае, когда в поле «часть сферы» выбрано 1/2. В остальных случаях, они не лежат в плоскости горизонта.
«Часть сферы» — выбор части сферы, из которой будет состоять купол. Для куполов разной частоты возможны различные пропорции отсечения.
Разветвление: уравнение сферы в координатах в пространстве
Рис. 13. Сфера с центром в точке
Выведем уравнение сферы радиуса с центром в точке (рис. 13).
Пусть произвольная точка лежит на сфере. Тогда, по определению сферы, . С другой стороны, расстояние между точками в координатах равно:
Приравнивая это к и возводя в квадрат, приходим к формуле, напоминающей уравнение окружности:
.
Это и есть уравнение сферы.
Соответственно, шар задается не уравнением, а неравенством:
.
Пример
Пусть дано уравнение . Требуется доказать, что данное уравнение задает сферу, и найти координаты ее центра и радиус.
Вспомним общее уравнение сферы:
Наша задача – свести исходное уравнение к уравнению сферы. Для этого выделим полные квадраты:
Таким образом, это действительно сфера, ее центр – точка с координатами , а ее радиус равен .
Рейтинг блогов и записей Живого Журнала
Расчет геодезического купола производится по заданному радиусу (площади поверхности основания), с целью получить:
- Расчетные размеры ребер и их количество
- Количество и тип требуемых коннекторов
- Значения углов между ребрами
- Требуемые высоту, общую площадь постройки
- Площадь поверхности купола
Площадь основания купола ассчитывается по заданному радиусу S=π *R2. При этом надо учитывать, что реальная площадь получится несколько меньше, вследствие того, что радиус купола считается, обычно, по внешней поверхности полусферы (по «вершинам»), и стенки купола имеют также определенную толщину.
| Геодезический купол — не чистая сфера, апроксимация приводит к тому, что в основании лежит не круг, а многоугольник, вписанный в заданную окружность. Площадь такого многоугольника заведомо меньше площади круга. |
Высота геодезического купола пределяется по заданному диаметру, и может быть для четной частоты разбиения 1/2, 1/4 диаметра (при большой частоте может быть и 1/6, 1/8). Для нечетной — 3/8, 5/8 диаметра (и т.д.).
| 4V, 1/4 сферы | 4V, 1/2 сферы |
Площадь поверхности геодезического купола ассчитывается по известной формуле расчета площади сферы S=4π *R2. Для купола, равного 1/2 сферы, формула будет иметь вид S=2π *R2. В более сложному случае, когда речь идет о площади сегмента, сферы, формула расчета S=2π *RH, где H — высота сегмента.Расчет конструктивных элементов геодезического купола ожно производить с использованием готовых таблиц, в которых заданы:
- Количество ребер купола одинаковой длины — ребра A, B, C, D, E, F, G, H, I. У купола с частотой 1V одно ребро — A. У купола с частотой 2V два ребра — A, B. У купола с частотой 3V три ребра — A, B, C. И т.д.
- Количство и тип используемых коннекторов — 4-х конечные, 5-ти конечные, 6-ти конечные.
- Коэффициенты пересчета длин ребер купола на радиус купола. К примеру, если вы хотите построить купол с частотой 2V высотой 1/2 и радиусом 3,5 метра, вам надо величину радиуса (3,5) умножить на коэффициент 0,61803 для определения длины ребра А, и умножить на коэффициент 0,54653 для определения длины ребра B. Получим: А=2,163м, В=1,912м.
1V купол
| Ребра | Коэффициенты | Количество |
| A | 1.05146 | 25 |
| 5-ти конечный коннектор | 6 | |
| 4-х конечный коннектор | 5 |
2V купол
| Ребра | Коэффициенты | Количество для 1/2 |
| A | 0,61803 | 35 |
| B | 0,54653 | 30 |
| 4-х конечный коннектор | 10 | |
| 5-ти конечный коннектор | 6 | |
| 6-ти конечный коннектор | 10 |
3V купол
| Ребра | Коэффициенты | Количество для 3/8 | Количество для 5/8 |
| A | 0,34862 | 30 | 30 |
| B | 0,40355 | 40 | 55 |
| C | 0,41241 | 50 | 80 |
| 4-х конечный коннектор | 15 | 15 | |
| 5-ти конечный коннектор | 6 | 6 | |
| 6-ти конечный коннектор | 25 | 40 |
4V купол
Геодезический купол своими руками
Добрый день! Эта статья будет полезна для всех, кому интересен геокупол, и кто хочет создать эту удивительную конструкцию своими руками. В статье мы не будем вдаваться в общую теорию геокуполов, т.к. это емкая тема, описанная в других статьях. Ниже приведены конкретные инструкции как сделать мобильный геокупол небольшого размера. Такой купол будет идеальным решением для всех путешественников и любителей жить на природе, подойдет для дачной беседки или детского домика. Данный купол — это универсальный мобильный шатер, компактный при транспортировке (подойдет для любой легковой машины), быстрый в сборке (2-3 часа), очень прочный и устойчивый к природным стихиям. А еще этот дом круглый и гармоничный. В народе поговаривают, что благодаря своей синергетической (геодезической) структуре каркаса, геокупол благоприятно влияет на окружающее пространство и гармонизирует его. В этом мы много раз убеждались на опыте. Установив в таком домике печь, можно смело жить в нем до поздней осени. Есть варианты для зимовки, но они требуют утепления. Многие фото материалы для этой статьи были собраны из разных источников, за что большая благодарность их создателям. Также отдельное спасибо латвийским друзьям, которые вдохновили нас на создание подобной инструкции.
Результаты измерений
Содержимое блока «результаты измерений» становится видимым при щелчке по заголовку этого блока «результаты измерений».
Блок с результатами измерений
Название каждого поля отвечает само за себя.
В блоке «Размеры» указано количество размеров и количество самих элементов:
«Граней» — первое число указывает количество размеров, второе число показывает количество граней. На схеме грани одного размера показаны одним цветом.
«Ребер» — первое число указывает количество размеров, второе число показывает количество рёбер. На схеме рёбра одного размера показаны одним цветом и обозначены одинаковыми буквами.
«Вершин» — первое число указывает количество вершин к которым подводятся разные рёбра без учета того, что к вершинам у снования подводится меньше рёбер. Второе число показывает количество вершин.
Исходные данные.
Область «Исходные данные» предназначена для задания геометрии каркаса. Можно изменять параметры в следующих полях:
«Многогранник» — многогранник на основание которого строится вся конструкция. Возможны два варианта: икосаэдр и октаэдр.
«Частота, V» — количество разбиений вершин. При увеличении частоты, увеличивается количество вершин и ребер соответственно. Чем больше это значение, тем больше форма каркаса приближается к сфере и тем меньше длина рёбер.
Икосаэдр — многогранник, у которого значение частоты разбиения V равно 1.Октаэдр — многогранник, у которого значение частоты разбиения V равно 1.
Значение частоты разбиения равное единице соответствует конструкции в виде икосаэдра или октаэдра в зависимости от того какой многогранник задан в графе «многогранник». При увеличении частоты происходит разбиение рёбер многогранника на части. Количество рёбер, составляющих разбитое ребро, равно частоте разбиения.
Частота разбиения икосаэдра.
«Класс разбиения» — этот пункт отвечает за выбор способа разбиения, а следовательно и формы конечной конструкции.
При частоте разбиения равной двум и более возможны различные варианты каждого разбиения. Эти варианты делятся на классы. Если спроецировать разбиение на грань икосаэдра, то все возможные классы разбиения икосаэдра можно представить в виде схемы.
Классы разбиения купольных конструкций.
В калькуляторе римскими цифрами обозначены основные классы, всего их три. Арабскими цифрами обозначены вариации основных классов.
Аналогично способы разбиения задаются для октаэдра.
«Метод разбиения» — позволяет сделать выбор между «Равные хорды», «Равные дуги», «Мексиканец» и «Крушке».
«Осевая симметрия» — выбор оси симметрии, которая учитывается при отсечении части купола от сферы и выстраивании купола по вертикали. Возможные варианты:
- Pentad — ось симметрии проходит через вершину, в которой сходится 5 рёбер для икосаэдра или 4 ребра для октаэдра.
- Cross — ось симметрии проходит через вершину, в которой сходится 6 рёбер.
- Triad — ось симметрии проходит через грань.
«Фулерен» — выбор формы купола в виде фулерена, который вписывается («вписанный») в сферу, или описывает её («описанный»). Поле «Фулерен» не доступно при выборе варианта соединения «Joint».
купол в форме фулерена
«Выравнивание основания» — позволяет выравнивать основание относительно плоскости основания за счет изменения длин рёбер у основания купола. Поле «Выравнивание основания» не доступно при выборе способа соединения «Cone» или выборе формы фулерена.
Функция «выравнивание основания» изменят длину рёбер у основания купола таким образом, что вершины купола на внешней его поверхности располагаются в плоскости основания. Вершины купола на внутренней поверхности купола в общем случае не располагаются в плоскости основания, а строятся по общему принципу — к центру купола от его внешней поверхности.
При включении «выравнивания основания» рёбра своей широкой стороной лежат в плоскости горизонта в случае, когда в поле «часть сферы» выбрано 1/2. В остальных случаях, они не лежат в плоскости горизонта.
«Часть сферы» — выбор части сферы, из которой будет состоять купол. Для куполов разной частоты возможны различные пропорции отсечения.
Основные достоинства
Одно из основных достоинств каркаса геодезического купола заключается в его надежности. Если при каких-либо обстоятельствах разрушится 35 % всей конструкции, каркас останется устойчивым. Такие постройки подходят для районов с повышенной сейсмической активностью, либо тех, где высокая вероятность ураганов и прочих природных явлений, угрожающих зданиям и сооружениям.
Устойчивость такой конструкции идеально подходит для размещения любых проемов в любом ее месте. С легкостью можно убрать несколько перемычек, и это не повлияет на надежность дома-купола. Окна такой конструкции будут в форме треугольника.
Обшивать постройку следует после полной установки каркаса, т. к. такой каркас имеет хорошие показатели скручиваемости, но плохо переносит горизонтальные нагрузки.
Примеры и разновидности купольных конструкций
Сферическую конструкцию можно построить двумя способами:
- В виде геодезического купола (собирается из треугольных каркасных ячеек, стыкуемых с помощью узловых элементов — коннекторов).
- Из гнутых стоек или сегментов арочной формы, соединяемых вершинами (стратодезический купол).
Геодезический купол
Стратодезический купол
Гнутоклееные деревянные стойки для сборки стратодезического купола
По технологии стратодезического купола собирают «маковки» православных храмов. Геодезический купол пришел к нам из Америки. Его изобретателем считают инженера Фуллера.
Несмотря на различия во внешнем виде, эти конструкции отличаются минимальным весом, высокой жесткостью и устойчивостью.
Дома в форме сферы можно строить из любого материала, начиная от пенопласта и заканчивая бетоном. Выбор конкретного варианта зависит от технической оснащенности исполнителя. Для возведения жилых зданий чаще всего используют конструкции с деревянным каркасом.
Причин для этого несколько. Древесина – экологичный и прочный материал, обладающий высокой упругостью. Геодезические купола собирают из деревянных балок, соединяя их стальными коннекторами.
Каркас дома на основе геодезического купола
Стратодезические жилые конструкции строят из гнутоклееных балок.
Каркас здания на основе стратодезического купола
Японская технология сферических зданий основана на использовании гнутых пенопластовых блоков с замками. Из них собирают небольшие одноэтажные постройки. Пенопласт в таком доме выполняет сразу две функции: конструкционного материала и утеплителя.
Современный домик-«иглу» строится не из снега, а из пенопластовой «скорлупы»
Минимальный вес дома-сферы позволяет возводить его на мелкозаглубленном ленточном или свайном фундаменте. Для утепления секций используют минвату, солому, эковату или пенопласт.
Наиболее распространенный вид кровельного покрытия – мягкая битумная черепица. Этот материал идеально ложится на криволинейные поверхности.
Дом-сфера, покрытый битумной черепицей
Сторонники экостроительства делают выбор в пользу деревянного гонта – тонких дощечек, образующих оригинальное чешуйчатое покрытие.
Деревянный гонт естественно смотрится на сферическом здании
Двухуровневый дом на основе стратодезического купола с гонтовой облицовкой
Недавно на рынке появились новые материалы, идеально адаптированные для создания бесшовного кровельного ковра. Это «жидкая пробка» (частицы пробкового дерева в акриловом полимере) и жидкая резина.
Как мы уже говорили, материал для строительства сферического дома может быть разнообразным. Если вам больше нравится бетон, нет проблем.
Используя технологию набрызга, можно возводить купольные постройки из легкого бетона
Современные технологии позволяют строить такие дома с помощью пневмоопалубки из ПВХ, на которую наносится вспененный утеплитель. Затем по утеплителю ставят арматурный каркас и наносят на него бетонную смесь методом торкретирования.
Из одних соломенных блоков дом-сферу не построишь. Этот материал используют как утеплитель. Солому плотно набивают в ячейки из досок и собирают из них купол.
Пространственный каркас выполнен из деревянных ячеек, наполненных соломой
В чём сила?
Как и обычная форма купола, конструкция Фуллера имеет хорошую устойчивость.
Распределение веса происходит равномерно, за счёт чего геокупол способен выдерживать значительные нагрузки.
За счёт этого можно сэкономить значительные средства на возведении фундамента. К тому же использование этого сооружения позволяет существенно уменьшить размеры стен сооружения.
За счёт особой формы купольная конструкция может хорошо противостоять даже сильным порывам ветра. Также не приходится сомневаться в хорошей устойчивости при возникновении подземных толчков. Благодаря чему дом купол можно построить даже в самой сейсмоопасной зоне.
Благодаря закруглённым стенам внутри здания с такой крышей создаётся идеальный микроклимат. Неслучайно такие сооружения считаются экологическими.
Помимо того что не требуется сооружать прочное основание, монтаж куполообразных объектов позволяет обходиться без специальной строительной техники, что заметно сокращает сроки строительства.
Не стоит забывать и про эстетичность. Геодезический купол отличается редкой красотой. Возможно, в недалёком будущем все здания и сооружения, включая жилые дома, обзаведутся купольной крышей.
Что собой представляет купольная теплица
Купольная теплица или, как ее называют по-другому, геокупол – это сферическая конструкция, напоминающая собой огромную полусферу. Сооружение строится за счет тщательного соединения множества треугольных или шестиугольных сегментов в единое целое. Это своеобразная «сетчатая» оболочка, треугольные или многоугольные элементы которой собираются из деталей различной длины. Многоугольными элементы геокупола бывают крайне редко, поэтому будем говорить о треугольных сегментах.
Купольная теплица по своему внешнему виду напоминает беседку, благодаря чему порой выступает в качестве не только полезного, но и декоративного сооружения на даче. Это строение имеет современный стиль и приятный дизайн.
Покрывают купольную теплицу различными материалами – полиэтиленом, сотовым поликарбонатом, стеклом. Оптимальный вариант – это, конечно же, поликарбонат.
Поликарбонат обладает массой преимуществ — в частности, он:
- крепкий и надежный;
- обладает хорошей светопропускной способностью;
- отлично удерживает тепло;
- легок в обработке и режется простым ножом;
- не боится холодов;
- способен защитить растения от ультрафиолета.
Каркас тепличного геокупола может быть выполнен из дерева, пластика, металла. Конечно, самым надежным вариантом является оцинкованная сталь, но своими руками проще собрать каркас из дерева – его проще обрабатывать, чем металл. К тому же дерево более экологично, но требует принятия более значительных защитных мер, чем тот же металл. Пластик – наименее прочный материал и служит меньше, но зато не боится практически никаких химических воздействий.
Интересно, что купольная теплица может иметь практически любой размер, при этом конструкция будет надежной и устойчивой даже без дополнительных подпорок. Однако оптимальным для небольшого дачного участка будет диаметр купола 4 м, а его высота — 2 м.
Схема купола
В правой части калькулятора отображается схема заданного купола. Купол можно вращать мышкой и приближать и отдалять его колесом мыши.
В калькуляторе можно посмотреть: каркас, кровлю, схему и план, нажав соответствующую кнопку. Их также можно вращать, увеличивать и уменьшать.
Кровля
Разными цветами показаны грани кровли различных размеров
Схема на вкладке «Кровля» позволяет исключать из расчёта отдельные грани и рёбра конструкции. Для исключения грани, нужно щёлкнуть по ней мышкой. Для исключения ребра нужно исключить примыкающие к нему с обеих сторон грани.
При исключении из расчёта граней и рёбер во вкладке «Кровля» значения в других вкладах и разделах калькулятора пересчитываются автоматически.
Данная функция может быть полезна для анализа возможных проёмов в конструкции, например для дверей и окон. А также для расчёта таких конструкций как беседки, навесы, козырьки и другие.
План
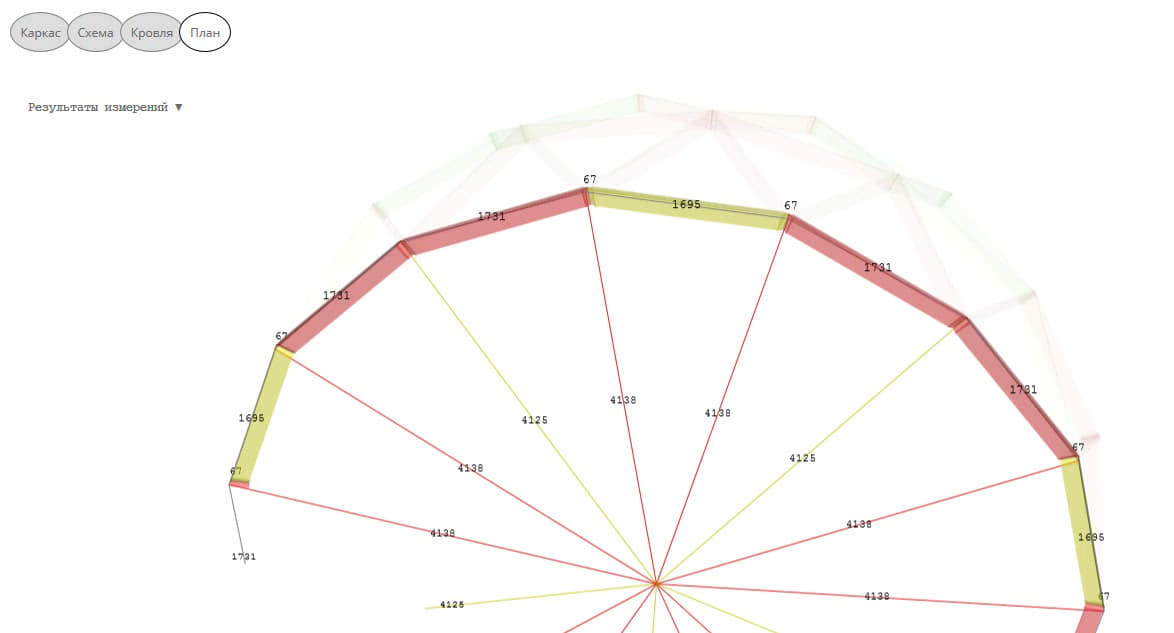На плане приведена проекция вершин купола на плоскость проходящую через основание купола
Во вкладке «План» можно увидеть проекцию нижних рёбер конструкции на плоскость в основании. А также размеры от центра сферы до концов проекций и высоту концов рёбер.
Выделив мышкой отдельные рёбра, можно увидеть аналогичную информацию для любого ребра купола.
Повторный щелчок мыши снимает выделение.
Если во вкладке «Кровля» исключена грань купола, то при переходе на вкладку «План» автоматически подсветятся рёбра этих граней.
Чтобы увидеть план основания полностью, вращайте схему курсором.
Размеры и способ соединения
Поле «размеры и способы соединения» позволяет задать размеры сферы и выбрать способ соединения ребер купола. Параметры поля:
«Радиус сферы, м
» — задается радиус сферы.
В выпадающем списке можно выбрать следующие варианты соединений:
- «Piped» — способ соединения с использованием коннекторов. При выборе данного способа соединений появляется дополнительное поле, в котором можно задать диаметр трубы, составляющей коннектор.
- «GoodKarma» — безконнекторный способ соединения, при котором каждое ребро составляют два бруса. При выборе данного способа соединения появляется дополнительное поле, в котором можно задать способ соединения рёбер по часовой стрелке или против часовой стрелки.
- «Semikone» — безконнекторный способ соединения, при котором каждое ребро составляют два бруса.
- «Cone» — безконнекторный способ соединения, при котором каждое ребро состоит из одного бруса.
- «Joint» — безконнекторный способ соединения, при котором каждое ребро состоит из одного бруса. При выборе данного способа соединения появляется дополнительное поле, в котором можно задать способ соединения рёбер по часовой стрелке или против часовой стрелки. Способ «Joint» не доступен для купола в форме фулерена.
- «Nose» — безконнекторный способ соединения, при котором каждое ребро состоит из одного бруса. Возможность выбора данного способа соединения предусмотрена только для купола в форме фулерена. Чтобы данный способ соединения появился в списке вариантов соединения, нужно предварительно задать форму купола в виде фулерена в поле «Фулерен» в разделе «Исходные данные». Для этого в поле «Фулерен» нужно выбрать один из вариантов: «Вписанный» или «Описанный». При выборе данного способа соединения появляется дополнительное поле, в котором можно задать способ соединения рёбер по часовой стрелке или против часовой стрелки.
Для всех способов соединения рёбра у основания купола состоят из одного бруса.
Подготавливаем участок для монтажа геодезического купола
Подбор участка под построение купольной теплицы производится аналогично подбора места для любых других дачных построек – стараетесь, чтобы место было хорошо освещено. Строительная площадка тщательно очищается от мусора и ненужных предметов, а затем хорошо разравнивается.
При желании поставить купольную теплицу на фундамент (это может случиться, если вы решили строить ее, используя тяжелые стеклопакеты), то сначала необходимо разметить участок и вырыть траншею. Надобность в рытье траншеи отпадет, если вы будете использовать металлические сваи.
Если вы не планируете устанавливать теплицу на фундамент, покрываете дно будущего строения защитным материалом для того, чтобы сорняки не прорастали в теплице. Затем на материал насыпаете большой слой гравия. Площадка под теплицу должна иметь ровное дно.
Основные виды геодезических конструкций
Конструкции геокуполов отличаются друг от друга частотой разбиения поверхности сферы на треугольники. Частоту разбиения принято обозначать буквой V. Число, стоящее рядом с V, показывает количество различных конструктивных элементов (ребер), используемых для построения каркаса. Чем больше число ребер используется, тем прочнее получается геокупол.
Существует шесть видов геокуполов, из которых активно применяются при строительстве объектов только пять:
- 2V купол (высота сооружения равна половине сферы);
- 3V купол (высота сооружения равна 5/8 сферы);
- 4V купол (высота сооружения равна половине сферы);
- 5V купол (высота сооружения равна 5/8 сферы);
- 6V купол (высота сооружения равна половине сферы).
Легко заметить, что полусферическая форма объекта достигается лишь при четной частоте разбиения.
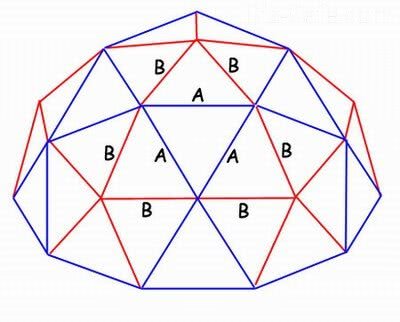
Схема каркаса геодезического купола типа 2V для создания небольших сооружений. Разные по длине ребра выделены цветом и обозначены буквами
Для небольших дачных построек обычно выбирается конструкция 2V купола. Каркас собирают из двух видов ребер, обозначающихся на схемах для удобства латинскими буквами A и B, а также выделяющихся дополнительно синим и красным цветом. Заготовки также помечают цветом, чтобы упростить процесс сборки каркасной конструкции. Для соединения отдельных ребер каркаса геодезического купола применяют специальные узлы, называемые коннекторами. При монтаже 2V-купольной конструкции используются три вида коннекторов:
- 4-х конечные;
- 5-ти конечные;
- 6-ти конечные.
Для подсчета длины ребер и количества коннекторов используют онлайн-калькуляторы, в которые забивают исходные данные объекта: радиус основания, частоту разбиения, желаемую высоту купола.
Три типа коннекторов, используемых для соединений ребер каркаса купола, сходящихся в одной точке (вершине многоугольника)
Большие полусферические объекты, диаметр основания которых превосходит 14 метров, строят с помощью 3V и 4V куполов. При меньшей частоте разбиения получаются слишком длинные ребра, что затрудняет их заготовку и монтаж. При постройке 3V купола длина ребер составляет почти три метра. Собирать каркас из таких длинномерных материалов довольно проблематично.
Выбрав другой тип купола (4V), уменьшают длину ребер до 2,27 метра, что существенно упрощает сборку купольного сооружения. Уменьшение длины конструктивных элементов ведет к увеличению их количества. Если у 3V купола при высоте 5/8 сферы насчитывается 165 ребер и 61 коннектор, то у 6V купола при той же высоте ребер уже 555 штук, а коннекторов – 196.
Свайный фундамент для установки больших купольных конструкций позволяет обеспечить сооружению необходимую прочность и устойчивость
Краткие сведения о купольной теплице
В купольной теплице не нужен дополнительный подогрев – температура имеет необходимое значение. Внешняя и внутренняя среда различны по температуре. Это обеспечивается способностью лучей солнца к нагреву грунта внутри купола, когда они проникают сквозь прозрачное покрытие «крыши». Происходит нагревание воздуха в теплице над самой почвой, благодаря подачи снизу тепла.
Ограждение купола также нагревается, добавляя тепла. Воздушные массы постоянно циркулируют под куполом, перенося это тепло. Перемещение теплого воздуха происходит снизу-вверх – грунтовая поверхность нагревается, нагреваются и находящиеся в теплице предметы.
По ночам и вечерам циркуляция воздуха производится сверху-вниз, спускаясь по остывшей поверхности теплицы. Воздушные массы, которые находятся вне теплицы, не нагреваются достаточно, поскольку активно движутся. Под куполом же они как будто попадают в зависимость от прозрачной оболочки теплицы.
Купольная теплица отличается тем, что она не восприимчива к любым неблагоприятным влияниям окружающей среды. Благодаря своей обтекаемой форме, теплица отлично противостоит сильным ветрам, кроме того, собранная из секций, конструкция ее достаточно сейсмоустойчивая.
